Welcome to modclock repo

Read Me here: https://bseib.github.io/modclock/

I put together these web pages to illustrate and demo some concepts around RSA encryption. There is a “modulus clock” page that will walk a circle, mod n. The other page can create multiple power mod calculators, to do the basic work to show RSA. These calcualtors can also be annotated to show where numbers are coming from.

Mod Power Calculators Page

https://bseib.github.io/modclock/modexp.html

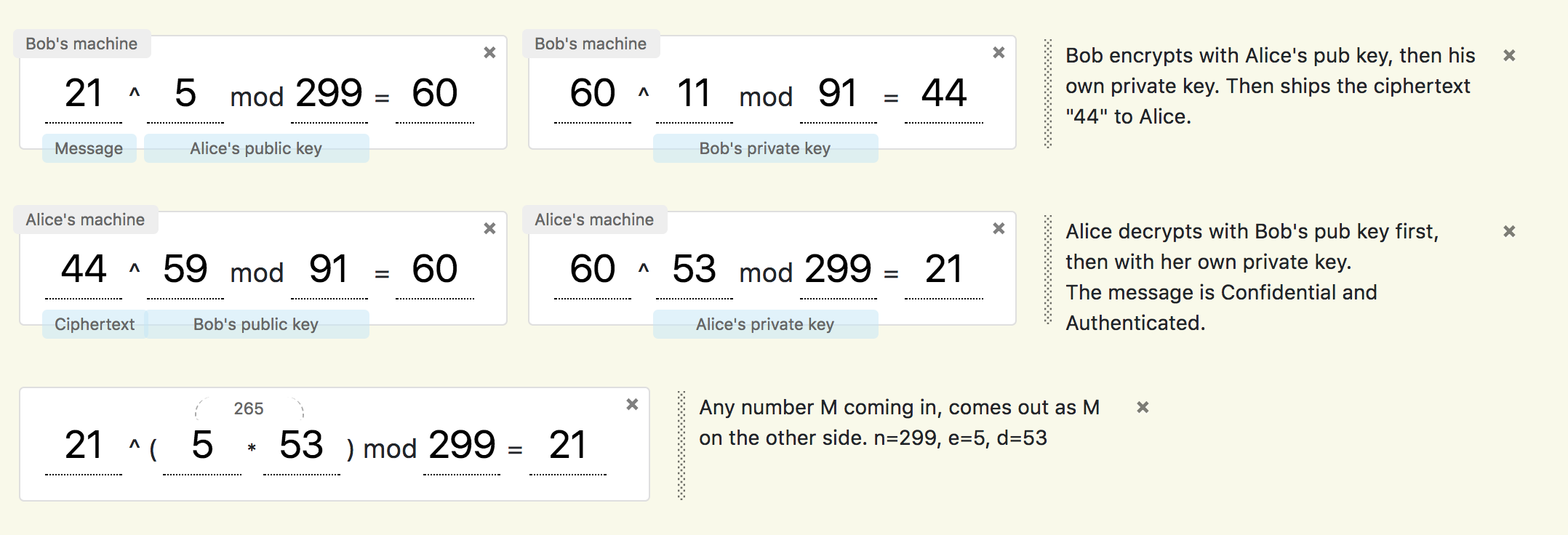
Click the new solver link at the top to get a new solver added to the page. This will solve a basic power mod equation of the form B^e mod n.

There are three “hot spots” you can click on to type in labels. One in the upper left corner, one below the input B, and one below the e and mod n area. There is also an × in the upper right to dismiss the calculator and remove it from the screen.

Also, for the Base and exponent fields, if you press the h key it will toggle the number as hidden, showing purple squares instead of digits. Used for the dramatic reveal!

Click the new solver2 link at the top to get a variation of a solver – one that solves the form B^e*d mod n. It also computes and displays the product of e*d after values are supplied. Good for illustrating putting M in and getting M back out.

Click the comment link at the top to add a comment field to the screen. You can click in the comment area and type what ever you want. Comment blocks are dismissable too.

Note: All the input fields are type=”number”, meaning you can use the up and down arrow keys to quickly cycle through different input values. This is useful when demonstrating M^(e*d)mod n = M. You can use arrow keys to show that no matter what you stick in, you get the same value back out.

Mod Clock Page

https://bseib.github.io/modclock/modclock.html

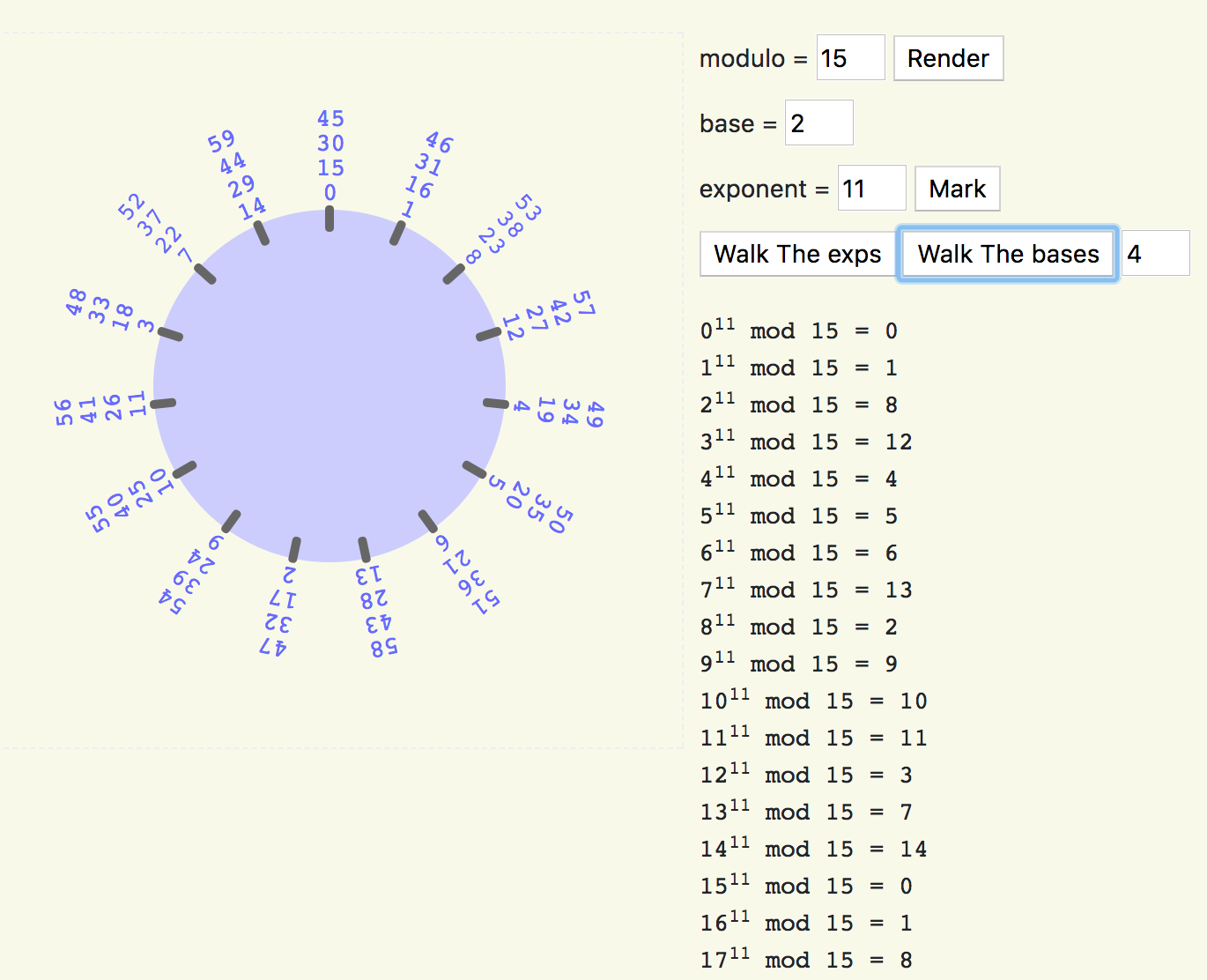
The modclock page lets you directly see where the exponent calculations fall before you apply the mod operation. If you supply a modulus (n), and an exponent, you can click “walk the bases” button and it will compute the answer for each base from 0 to n and plot it on the circle. If you increase the integer to the right of the “walk the bases” button, it will actually continue to walk the bases another round, showing the exponent values before the modulo operation, but showing that they will fall on the same answer as their predecesor.

The Render button will draw the circle again, clean slate.

The Mark button will compute the answer for the current values of n, B, and e and plot that one answer.

Hack Lafayette Thunder Talks

Here are the slides I presented at Hack Lafayette’s December 2017 Thunder Talks.